Основное уравнение движения электропривода. Уравнение движения электропривода, ввод т анализ Самая главная суть уравнения движения электропривода

Механическая часть электропривода представляет собой систему твёрдых тел, движение которых определяется механическими связями между телами. Если заданы соотношения между скоростями отдельных элементов, то уравнение движения электропривода имеет дифференциальную форму. Наиболее общей формой записи уравнений движения являются уравнения движения в обобщенных координатах (уравнения Лагранжа):

W k – запас кинетической энергии системы, выраженный через обобщенные координаты q i и обобщенные скорости ;

Q i – обобщенная сила, определяемая суммой работ δA i всех действующих сил на возможном перемещении .

Уравнение Лагранжа можно представить в другом виде:

(2.20)

Здесь L – функция Лагранжа, представляющая собой разность кинетической и потенциальной энергий системы:

L = W k – W n .

Число уравнений равно числу степеней свободы системы и определяется числом переменных – обобщенных координат, определяющих положение системы.

Запишем уравнения Лагранжа для упругой системы (рис. 2.9).

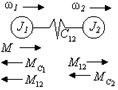
Рис. 2.9. Расчетная схема двухмассовой механической части.

Функция Лагранжа в этом случае имеет вид

Для определения обобщенной силы необходимо вычислить элементарную работу всех приведённых к первой массе моментов на возможном перемещении:

Следовательно, т.к. обобщенная сила определяется суммой элементарных работ δA 1 на участке δφ 1 , то для определения величины получим:

Аналогично, для определения имеем:

Подставив выражение для функции Лагранжа в (2.20), получим:

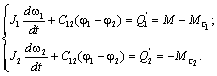
Обозначив , получим:

(2.21)

Примем механическую связь между первой и второй массами абсолютно жёсткой, т.е. (рис. 2.10).

Рис. 2.10. Двухмассовая жесткая механическая система.

Тогда и второе уравнение системы примет вид:

Подставив его в первое уравнение системы, получим:

(2.22)

Это уравнение иногда называют основным уравнением движения электропривода. С его помощью можно по известному электромагнитному моменту двигателя М, моменту сопротивления и суммарному моменту инерции оценить среднее значение ускорения электропривода, рассчитать время, за которое двигатель достигнет заданной скорости, и решить другие задачи, если влияние упругих связей в механической системе существенно.

Рассмотрим механическую систему с нелинейными кинематическими связями типа кривошипно-шатунных, кулисных и других подобных механизмов (рис. 2.11). Радиус приведения в них является переменной величиной, зависящей от положения механизма: .

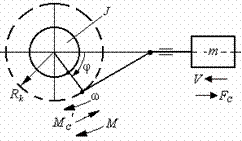
Рис. 2.11. Механическая система с нелинейными кинематическими связями

Представим рассматриваемую систему в виде двухмассовой, первая масса вращается со скоростью ω и имеет момент инерции , а вторая движется с линейной скоростью V и представляет суммарную массу m элементов, жёстко и линейно связанных с рабочим органом механизма.

Связь между линейными скоростями ω и V нелинейная, причём . Для получения уравнения движения такой системы без учёта упругих связей воспользуемся уравнением Лагранжа (2.19), приняв в качестве обобщенной координаты угол φ. Определим обобщенную силу:

Суммарный момент сопротивления от сил, воздействующих на линейно связанные с двигателем массы; приведённый к валу двигателя;

F C – результирующая всех сил, приложенная к рабочему органу механизма и линейно связанным с ним элементам;

– возможное бесконечно малое перемещение массы m .

Нетрудно видеть, что

Радиус приведения.

Момент статической нагрузки механизма содержит пульсирующую составляющую нагрузки, изменяющуюся в функции угла поворота φ:

Запас кинетической энергии системы:

Здесь - суммарный приведённый к валу двигателя момент инерции системы.

Левую часть уравнения Лагранжа (2.19) можно записать в виде:

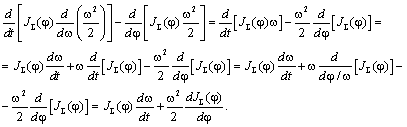
Таким образом, уравнение движения жёсткого приведённого звена имеет вид:

(2.23)

Оно является нелинейным с переменными коэффициентами.

Для жёсткого линейного механического звена уравнение статического режима работы электропривода соответствует и имеет вид:

Если при движении то имеет место или динамический переходный процесс, или принуждённое движение системы с периодически изменяющейся скоростью.

В механических системах с нелинейными кинематическими связями статические режимы работы отсутствуют. Если и ω=const, в таких системах имеет место установившийся динамический процесс движения. Он обусловлен тем, что массы, движущиеся линейно, совершают возвратно-поступательное движение, и их скорости и ускорения являются переменными величинами.

С энергетической точки зрения различают двигательные и тормозные режимы работы электропривода. Двигательный режим соответствует прямому направлению передачи механической энергии к рабочему органу механизма. В электроприводах с активной нагрузкой, а также в переходных процессах в электроприводе, когда происходит замедление движения механической системы, происходит обратная передача механической энергии от рабочего органа механизма к двигателю.

Расчетная схема механической части электропривода

Механика электропривода

Электропривод представляет собой электромеханическую систему, состоящую из электрической и механической части. В этой главе мы рассмотрим механическую часть ЭП.

В общем случае механическая часть ЭП включает в себя механическую часть электромеханического преобразователя (ротор или якорь электродвигателя), преобразователь механической энергии (редуктор или механическую передачу) и исполнительный орган рабочей машины (ИО РМ). Поскольку наша задача - это приведение в движение ИО РМ, основополагающими для выбора и расчета ЭП являются характеристики рабочей машины и особенности механической части ЭП .

В общем случае механическая часть ЭП представляет собой сложную механическую систему, состоящую из нескольких вращающихся и поступательно движущихся с различными скоростями звеньев, имеющими различные массы и моменты инерции, соединенные упругими связями (малой или конечной жесткости). При этом в кинематических передачах часто имеют место зазоры.

На эту сложную механическую систему действуют различные по направлению и величине внешние моменты и силы, которые, в свою очередь, часто зависят от времени, угла поворота механизма, скорости движения и других факторов. Поскольку эта механическая система является неотъемлемой частью ЭП, необходимо знать её характеристики и иметь достаточно точное для инженерных расчетов математическое описание. Механическая часть ЭП описывается в общем случае системой нелинейных дифференциальных уравнений в частных производных с переменными коэффициентами. Для описания механической части ЭП наиболее удобным является использование уравнений Лагранжа второго рода.

Учитывая, что движение механической системы определяется наибольшими массами, наименьшими жесткостями и наибольшими зазорами; очень часто сложную механическую систему можно свести к двух-трех- массовой модели, которая может быть использована при расчете систем ЭП. (Это системы с гибкими валами, системы, подверженные резким динамическим нагрузкам, точные следящие системы).

В большинстве случаев механическая часть состоит из звеньев большой жесткости с жесткими связями, а зазоры мы стремимся свести к нулю, и тогда возникает возможность представить расчетную схему механической части как одномассовую систему, укрепленную на валу ЭД, при этом мы пренебрегаем упругостью механических связей и зазорами в передаче. Такая модель широко применяется для инженерных расчетов.

Для анализа движения механической части ЭП осуществляется переход от реальной кинематической схемы к расчетной, в которой массы и моменты инерции движущихся элементов их жесткости, а также силы и моменты, действующие на эти элементы, заменены эквивалентными величинами, приведенными к одной и той же скорости (чаще всего к скорости движения ЭД). Условием соответствия полученной расчетной схемы реальной механической части ЭП является выполнение закона сохранения энергии.

Рис. 2.1. Кинематическая схема подъемного устройства

Переход от реальной схемы (рис. 2.1) к расчетной (рис. 2.2) называют приведением. Все параметры механической части приводят к валу ЭД (в некоторых случаях к валу редуктора).

Рис. 2.2. Расчетная схема подъемного устройства

Приведение моментов инерции и масс осуществляется с помощью следующих известных из механики формул:

Для вращательного движения, (2.1)

Для поступательного движения, (2.2)

Суммарный момент инерции системы, (2.3)

где – момент инерции двигателя, кг∙м 2 ;

– момент инерции k-ого вращающегося элемента, кг∙м 2 ;

– масса i-ого поступательно движущегося элемента, кг;

, – приведённые моменты инерции k и i элементов, кг∙м 2 .

Моментом инерции тела относительно оси, проходящей через центр тяжести, называют сумму произведений массы каждой элементарной частицы тела на квадрат расстояния от соответствующей частицы до оси вращения

где R j – радиус инерции

i k – передаточное число кинематической цепи между валом двигателя и k-ым элементом,

– угловые скорости вала двигателя и k-ого элемента, с -1 .

где – радиус приведения поступательно движущегося i элемента к валу двигателя, м,

– скорость движения поступательно движущегося i элемента, м/с.

Радиусом инерции называют расстояние от оси вращения (проходящей через центр тяжести), на котором надо поместить массу рассматриваемого тела, сосредоточенную в одной точке, чтобы удовлетворить равенство

Приведение моментов и сил , действующих на элементы к валу двигателя, осуществляются следующим образом:

Первый вариант: передача энергии от двигателя к рабочей машине

Для вращательно движущихся элементов, (2.6)

Для поступательно движущихся элементов. (2.7)

Второй вариант: энергия передается от рабочей машины к двигателю

Для вращательно движущихся элементов, (2.8)

Для поступательно движущихся элементов. (2.9)

В этих выражениях:

– момент, действующий на k элемент, Н∙м;

– сила, действующая на i элемент, Н;

– приведённый момент (эквивалентный), Н∙м;

– КПД кинематической цепи между k и i элементом и валом двигателя.

С помощью приведенных расчётных схем осуществляется определение параметров, устойчивость и характер протекания переходных процессов в механической системе.

Динамику ЭП, как правило, определяет механическая часть привода как более инерционная. Для описания переходных режимов необходимо составить уравнение движения ЭП учитывающее все силы и моменты, действующие в переходных режимах .

Наиболее удобным методом составления уравнений движения механизмов является метод уравнений Лагранжа второго рода. Сложность уравнения движения будет зависеть от того, какую расчетную схему механической части привода мы выбрали. В большинстве практических случаев выбирают одномассовую, расчетную схему, сводя всю систему электродвигатель-рабочая машина (ЭД-РМ) к жесткому приведенному механическому звену.

Одномассовая система (жесткое приведённое звено) является интегрирующим звеном. В том случае, когда в кинематической цепи ЭП содержатся нелинейные связи, параметры которых зависят от положения отдельных звеньев механизма (пары кривошип – шатун, кулисный механизм и так далее) движение одномассовой системы описывается нелинейным дифференциальным уравнением с переменными коэффициентами. Входящие в это уравнение моменты в общем случае могут быть функциями нескольких переменных (времени, скорости, угла поворота).

Как следует из структурной схемы, момент двигателя представляет собой управляющее воздействие, а момент сопротивления - возмущающее воздействие.

Когда момент, развиваемый двигателем, равен моменту сопротивления исполнительного органа, скорость привода постоянна.

Однако во многих случаях привод ускоряется или замедляется, т.е. работает в переходном режиме.

Переходным режимом электропривода называют режим работы при переходе от одного установившегося состояния к другому, когда изменяются скорость, момент и ток.

Причинами возникновения переходных режимов в электроприводах является изменение нагрузки, связанное с производственным процессом, либо воздействие на электропривод при управлении им, т.е. пуск, торможение, изменение направления вращения и т.п., а также нарушение работы системы электроснабжения.

Уравнение движения электропривода должно учитывать все моменты, действующие в переходных режимах.

В общем виде уравнение движения электропривода может быть записано следующим образом :

При положительной скорости уравнение движения электропривода имеет вид

. (2.10)

Уравнение (2.10) показывает, что развиваемый двигателем вращающий момент уравновешивается моментом сопротивления и динамическим моментом . В уравнениях (2.9) и (2.10) принято, что момент инерции привода является постоянным, что справедливо для значительного числа исполнительных органов.

Из анализа уравнения (2.10) видно:

1) при > , , т.е. имеет место ускорение привода;

2) при < , , т.е. имеет место замедление привода (очевидно, замедление привода может быть и при отрицательном значении момента двигателя);

3) при = , ; в данном случае привод работает в установившемся режиме.

Динамический момент (правая часть уравнения моментов) проявляется только во время переходных режимов, когда изменяется скорость привода. При ускорении привода этот момент направлен против движения, а при торможении он поддерживает движение.

2.5. Установившееся движение и устойчивость
установившегося движения электропривода

Имея механическую характеристику двигателя и исполнительного органа, нетрудно определить выполнимость условия установившегося движения . Для этого совместим в одном и том же квадранте эти характеристики. Факт пересечения этих характеристик говорит о возможности совместной работы двигателя и исполнительного органа, а точка их пересечения является точкой установившегося движения, так как в этой точке и .

На рисунке 2.4 показаны механические характеристики вентилятора (кривая 1) и двигателя независимого возбуждения (прямая 2). Точка А является точкой установившегося движения, а ее координаты – координатами установившегося движения вентилятора.

Рис. 2.4. Определение параметров установившегося движения

Для полного анализа установившегося движения необходимо определить, является ли это движение устойчивым. Устойчивым будет такое установившееся движение, которое, будучи выведенным из установившегося режима каким-то внешним возмущением, возвращается в этот режим после исчезновения возмущения .

Для определения устойчивости движения удобно пользоваться механическими характеристиками.

Необходимым и достаточным условием устойчивости установившегося движения является противоположность знаков приращения скорости и возникающего при этом динамического момента, т.е.

Оценим в качестве примера (рис. 2.5) устойчивость движения электропривода. Установившееся движение возможно с двумя скоростями: в точке 1 и в точке 2, в которых . Определим, устойчиво ли движение в обеих точках.

Рис. 2.5. Определение устойчивости механического движения

Точка 1. Предположим, что под действием кратковременного возмущения скорость увеличилась до значения , после чего воздействие исчезло. По механической характеристике АД скорости будет соответствовать момент .

В результате этого динамический момент =станет отрицательным, и привод начнет тормозиться до скорости , при которой .

Если возмущение вызовет снижение скорости до значения , то мо­­-
мент АД возрастет до значения , динамический момент
= станет положительным, и скорость увеличится до прежнего значения . Таким образом, движение в точке1 со скоростью является устойчивым.

При проведении аналогичного анализа можно сделать вывод о неустойчивости движения электропривода в точке 2со скоростью .

Устойчивость или неустойчивость движения может быть определена и аналитически с помощью понятия жесткости механических характеристик АД и исполнительного органа: . Условие устойчивости :

или . (2.12)

Для рассматриваемого примера , поэтому устойчивость определяется знаком жесткости характеристики АД: для точки 1 движение устойчиво, а для точки 2 и движение неустойчиво.

Отметим, что в соответствии с уравнением (2.10) при определенной жесткости устойчивая работа электропривода возможна и при положительной жесткости механической характеристики АД, в частности, на так называемом нерабочем участке характеристики АД.

2.6. Неустановившееся движение электропривода
при постоянном динамическом моменте

Неустановившееся механическое движение электропривода возникает во всех случаях, когда момент двигателя отличается от момента нагрузки, т.е. когда .

Рассмотрение неустановившегося движения электропривода имеет своей основной целью получение зависимостей во времени выходных механических координат электропривода – момента , скорости и положение вала двигателя . Кроме того, часто требуется определить время неустановившегося движения (переходного процесса) электродвигателя. Отметим, что законы изменения моментов двигателя и нагрузки должны быть предварительно заданы.

Рассмотрим неустановившееся движение при постоянном динамическом моменте во время пуска электродвигателя. Предполагается, что во время пуска электродвигателя и , но .

Решая уравнение механического движения электропривода, получаем следующую зависимость :

; (2.13)

Уравнение (2.14) получено с учетом равенств и .

Полагая в уравнении (2.13) и , находим время изменения скорости от до

. (2.15)

Характеристики , , представлены на рисунке 2.6.

Рис. 2.6. Характеристики , ,
при пуске ЭД

В уравнениях (2.13), (2.14) и (2.15) момент принят равным среднему моменту при пуске двигателя, поэтому полученные выше аналитические соотношения используют только при выполнении различных приближенных расчетов в электроприводе. В частности, неустановившееся движение может быть рассмотрено при торможении и реверсе электропривода, или при переходе с одной характеристики на другую.

2.7. Неустановившееся движение электропривода
при линейной зависимости моментов двигателя
и исполнительного органа от скорости

Рассматриваемый вид движения является весьма распространенным.

На рисунке 2.7 представлены механические характеристики ЭД и ИО при пуске электродвигателя.

Рис. 2.7. Механические характеристики ЭД и ИО при пуске электродвигателя

Механические характеристики ЭД и ИО можно выразить аналитически следующими уравнениями:

В уравнениях (2.16) и (2.17) и – коэффициенты жесткости механических характеристик ЭД и ИО.

Подставляя выше приведенные уравнения в уравнение механического движения электропривода, получаем следующие уравнения для зависимостей , , .

где – электромеханическая постоянная времени в секундах, учитывающая механическую инерционность привода и влияющая на время пуска электропривода.

Полученные выражения (2.18)–(2.20) могут использоваться для анализа переходных процессов различного вида, но в каждом конкретном случае должна быть определена электромеханическая постоянная времени , а также начальные и конечные значения координат , , , . В частном случае, когда и , эти величины могут быть определены по формулам:

; (2.21)

; , (2.22)

где– это время, в течение которого электропривод запускается до скорости при . Тогда . Так как обычно момент двигателя при пуске изменяется, то на практике время пуска в секундах определяют по выражению , или по следующему выражению: .

Зависимости , приведены на рисунке 2.8.

Рис. 2.8. Зависимости ,
при пуске электродвигателя

2.8. Неустановившееся движение электропривода
при произвольной зависимости динамического момента
от скорости

При определении ; ; при сложных зависимостях
момента двигателя и момента сопротивления от скорости, пользуются численным методом Эйлера. Суть его в том, что в уравнении движения электропривода дифференциалы переменных и заменяются малыми приращениями
и .

Покажем использование метода Эйлера на примере пуска асинхронным электродвигателем центробежного насоса. Механические характеристики ЭД
и центробежного насоса приведены на рис. 2.9 .

Рис. 2.9. Механические характеристики ЭД и ИО

1. Ось скорости разбивают на малые и равные участки ∆ ω.

2. На каждом участке определяют средние моменты и т.д., и т.д.

3. Затем составляется таблица 2.1 и по ней определяют зависимости .

Таблица 2.1

ω 1 =∆ω 1			t 1 =∆t 1
ω 2 =ω 1 +∆ω 2			t 2 = t 1 +∆t 2
ω 3 =ω 2 +∆ω 3			t 3 =t 2 +∆t 3
…	…	…	…
ω n	М д n		t n

; и т.д.– угловые скорости ЭД и ИО; .

Коробки скоростей или механические вариаторы могут быть громоздкими (сложными). Их применение уменьшает надежность и КПД электропривода. Поэтому на практике в основном применяют электрический способ регулирования, воздействуя на параметры электродвигателя или источника питания. Этот способ имеет лучшие технико-экономические показатели. Однако на некоторых металлообрабатывающих станках применяют смешанный способ регулирования.

В теории электропривода механические, электрические и магнитные переменные, характеризующие работу двигателя, – скорость, ускорение, положение вала, момент, ток, магнитный поток и т.д. – часто называют координатами . Поэтому управление движением исполнительного органа электрическим способом осуществляется за счет регулирования координат (переменных) электродвигателя.

Существенно отметить, что регулирование координат электропривода должно осуществляться для управления как установившимся, так и неустановившимся движением исполнительного органа.

Типичным примером регулирования переменных может служить ЭП пассажирского лифта. При пуске и останове кабины для обеспечения комфортности пассажиров ускорение и замедление ее движения не должно быть выше допустимого уровня. Перед остановкой скорость кабины должна снижаться, т.е. она должна регулироваться. И, наконец, кабина с заданной точностью должна останавливаться на требуемом этаже, т.е. необходимо обеспечивать заданное положение (позиционирование) кабины лифта.

Пользуясь рассмотренным примером, отметим то важное обстоятельство, что часто электропривод должен обеспечить регулирование одновременно нескольких координат: скорости, ускорения и положения исполнительного органа.

При изготовлении бумаги, тканей, кабельных изделий, различных пленок, прокатке металлов требуется обеспечение определенного натяжения этих материалов, что также осуществляется с помощью ЭП. Регулирования координат требуют и многие другие рабочие машины и механизмы: подъемные краны, металлообрабатывающие станки, транспортеры, насосные агрегаты, роботы и манипуляторы и т.д.

Основное уравнение движения электропривода связывает между собой электромагнитный момент двигателя, момент статистический, момент интеграции и скорость вала двигателя.

Разность, записанная в левой части выражения, представляет собой динамический момент

Если динамический момент не равен 0, то электропривод работает в динамическом режиме т.е. имеет место изменение скорости.

Если или то электропривод работает в статическом (т.е. устанавливается) режиме работы.

ПОТЕРИ В МЕХАНИЧЕСКОЙ ПЕРЕДАЧЕ. КПД ПЕРЕДАЧИ

Потери энергии (мощности) в передаче учитывают двумя способами:

1) приближенным, т.е. с помощью КПД и 2) уточненным, т.е. непосредственным вычислением составляющих потерь. Рассмотрим эти способы.

А. Учет потерь в передачах с помощью КПД.

Механическая часть электропривода (рис.1.17) включает ротор электродвигателя ЭД с угловой скоростью w и моментом М, передаточный механизм ПМ, имеющий КПД h п и передаточное число j, и исполнительный механизм ИМ, на валу которого приложен момент М м и скорость вала w м. Для наглядности обозначим статический момент в двигательном режиме , а в тормозном - . Для двигательного режима работы, исходя из закона сохранения энергии, можно записать равенство

,
, где ,

- момент механизма, приведенный к валу электродвигателя.

Для тормозного режима будем иметь такое равенство

,
,

Но КПД является переменной величиной, зависящей от постоянных и переменных потерь в передаче. Определим потерю момента в передаче для двигательного режима

,

Примем допущение, что в тормозном режиме будет такая же потеря момента. Тогда статический момент в тормозном режиме можно записать в таком виде:

1) , тогда , что соответствует тормозному режиму, когда двигатель развивает тормозной момент. Применительно к грузоподъемному механизму это будет опускание тяжелого груза, когда момент от действия груза на валу двигателя М г превышает момент потерь DМ в передаче. Получаем так называемый тормозной спуск;

2) , тогда , что соответствует не тормозному, значит, двигательному режиму. Для грузоподъемного механизма это эквивалентно опусканию крюка, когда момент от его веса на валу двигателя М К меньше момента потерь DМ в передаче. Имеем так называемый силовой спуск.

Потери момента в передаче приближенно выражаются через две составляющие, одна из которой для данной передачи является постоянной величиной, а вторая – пропорциональна передаваемому моменту:

где – коэффициент постоянных потерь;

b – коэффициент переменных потерь;

М с.ном – номинальный статический момент передачи;

М перед – передаваемый момент, который равен моменту на выходном (по направлению передачи энергии) валу передачи.

Для установившегося двигательного режима . КПД передачи можно представить отношением мощностей в установившемся режиме.

суммой момента двигателя и момента сопротивления. В отдельных случаях момент двигателя, равно как и момент сопротивления, может быть направлен как в сторону движения ротора, так и против этого движения. Однако во всех случаях независимо от движущего или тормозного характера момента двигателя и момента сопротивления в задачах электропривода выделяются именно указанные составляющие результирующего момента. Последнее определяется тем, что чаще всего момент сопротивления задан заранее, а момент двигателя выявляется в процессе расчета и тесно связан с величинами токов в его обмотках, которые позволяют оценить нагрев двигателя.

В системах электропривода основным режимом работы электрической машины является двигательный. При этом момент сопротивления имеет тормозящий характер по отношению к движению ротора и действует навстречу моменту двигателя. Поэтому положительное направление момента сопротивления принимают противоположным положительному направлению момента двигателя, в результате чего уравнение (2.8) при J = const может быть представлено в виде:

Уравнение (2.9) называют основным уравнением движения электропривода. В уравнении (2.9) моменты являются алгебраическими, а нс векторными величинами, поскольку оба момента М и действуют относительно одной и той же оси вращения.

где угловое ускорение при вращательном движении.

Правую часть уравнения (2.9) называют динамическим моментом (), т. е.

Из (2.10) следует, что направление динамического момента всегда совпадает с направлением ускорения электропривода.

В зависимости от знака динамического момента различают следующие режимы работы электропривода:

Момент, развиваемый двигателем, не является постоянной величиной, а представляет собой функцию какой-либо одной переменной, а в некоторых случаях и нескольких переменных. Эта функция задается аналитически или графически для всех возможных областей ее изменения. Момент сопротивления также может быть функцией какой-либо переменной: скорости, пути, времени. Подстановка в уравнение движения вместо М и Л/с их функций приводит в общем случае к нелинейному дифференциальному уравнению.

Уравнение движения в дифференциальной форме (2.9) справедливо для постоянного радиуса инерции вращающейся массы. В некоторых случаях, например при наличии кривошипно-шатунного механизма (см. рис. 2.2, г), в кинематической цепи привода радиус инерции оказывается периодической функцией угла поворота. В этом случае можно воспользоваться интегральной формой записи уравнения движения, исходящей из баланса кинетической энергии в системе:

(2.11)

где J((o !/2) – запас кинетической энергии привода для рассматриваемого момента времени; 7,(0)^,/2) – начальный запас кинетической энергии привода.

Дифференцируя уравнение (2.11) по времени с учетом того факта, что 7 – функция угла поворота <р, получаем:

(2.12)

Так как , то, разделив (2.12) на угловую скорость <о, получим уравнение движения при 7 =J[ в следующем виде:

(2.13)

В ряде случаев целесообразно рассматривать движение на рабочем органе производственной машины (такие задачи часто возникают для подъемно-транспортных машин с поступательно движущимся рабочим органом). В этом случае следует использовать уравнения для поступательного движения. Уравнение движения электропривода для поступательного движения получают так же, как и для вращательного движения. Так при т = const уравнение движения принимает вид:

При т =f}